Clean Rounding to €0.05 with VAT
Purpose
In some scenarios, it is useful to adjust the tax-excluded price (HT) of a product or service so that the final tax-included price (TTC) rounds exactly to a multiple of €0.05. This “clean” rounding is especially relevant where price aesthetics or accounting simplicity is important, such as in point-of-sale environments.
Advantage of the Approach
This approach considers VAT multiplication upfront, ensuring that the final TTC price, once rounded to two decimal places, is an exact multiple of €0.05.
The trade-off is accepting a slight modification of the original HT price to achieve that clean result.
Next HT Multiple of €0.05
This function finds the next HT price that, when multiplied by the VAT rate, results in a TTC price that rounds to a multiple of €0.05.
SQL Function
CREATE OR REPLACE FUNCTION get_next_ht_multiple_05(ht numeric, taxes numeric)
RETURNS numeric AS $$
DECLARE
current_ht numeric := ceil(ht * 100) / 100;
ttc numeric;
steps integer := 0;
max_steps integer := 100;
BEGIN
LOOP
EXIT WHEN steps > max_steps;
ttc := round(current_ht * taxes, 2);
IF mod(ttc * 100, 5) = 0 THEN
RETURN current_ht;
END IF;
current_ht := current_ht + 0.01;
steps := steps + 1;
END LOOP;
RETURN ht; -- fallback if nothing is found
END;
$$ LANGUAGE plpgsql IMMUTABLE;
Example with 21% VAT
The get_next_ht_multiple_05 function is applied across a price range from €0.00 to €100.00, in steps of €0.01. For each HT price, we check if within the next 100 cents, there is a value that results in a TTC rounded to a multiple of €0.05.
VAT used: 1.21 (i.e., 21%) Criteria: round(HT × 1.21, 2) mod 0.05 = 0
Result
- Total tested: 10,001
- Unchanged (no adjustment needed): 2,001
- Adjusted HT prices: 8,000
- Maximum HT deviation: -€0.12
Deviation Analysis
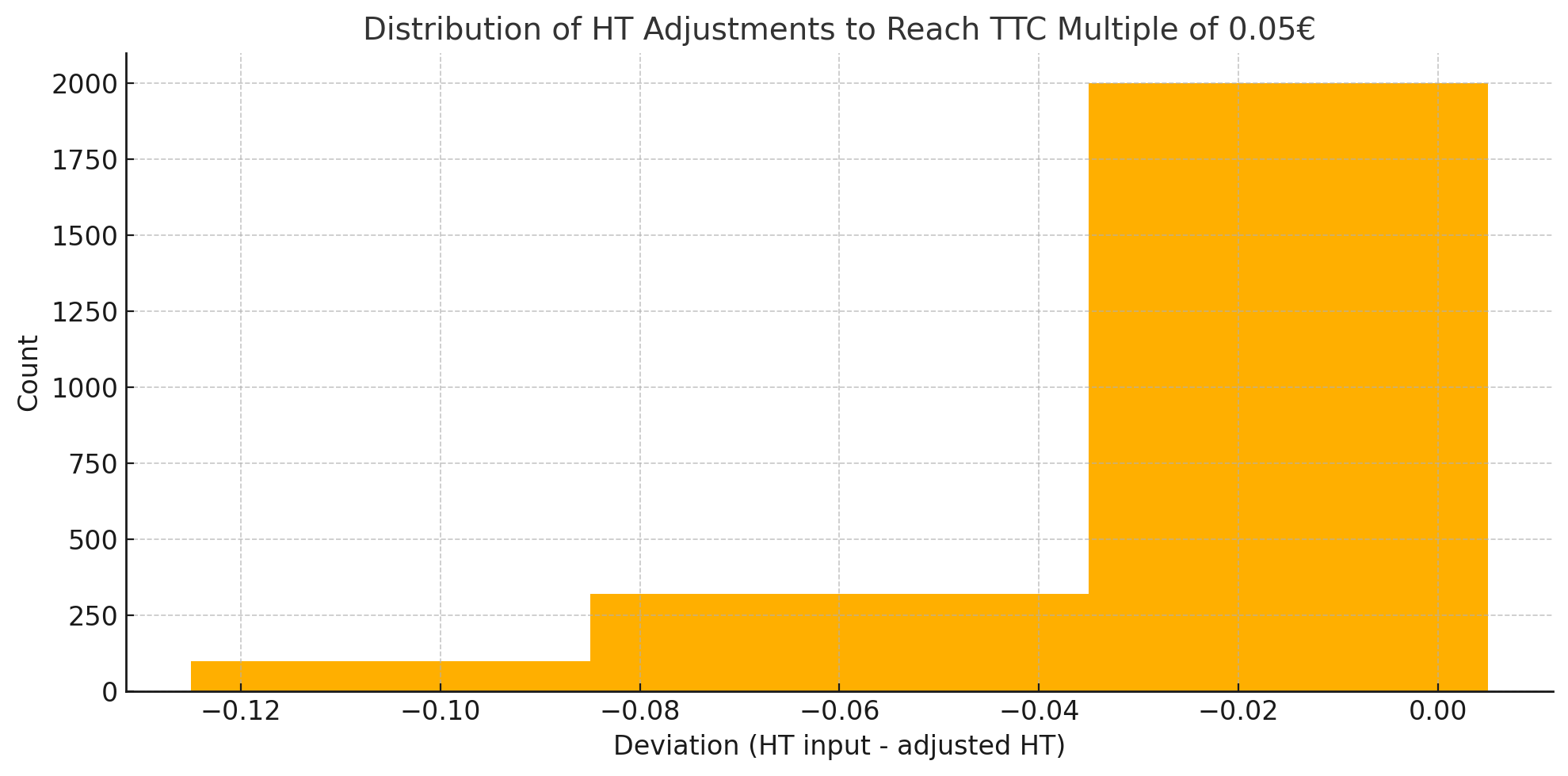
| Deviation | Count |
|---|---|
| -0.12 | 100 |
| -0.11 | 100 |
| -0.10 | 100 |
| -0.09 | 100 |
| -0.08 | 320 |
| -0.07 | 320 |
| -0.06 | 320 |
| -0.05 | 320 |
| -0.04 | 320 |
| -0.03 | 2,000 |
| -0.02 | 2,000 |
| -0.01 | 2,000 |
| 0.00 | 2,001 |
Nearest HT Multiple of €0.05
A more advanced version could search in both directions (up and down) to find the closest TTC-rounded price to the original HT.
This would minimize deviation from the original HT while still achieving the goal of clean TTC rounding.
SQL Function
CREATE OR REPLACE FUNCTION get_nearest_ht_multiple_05(ht numeric, taxes numeric)
RETURNS numeric AS
$$
DECLARE
step numeric := 0.01;
i integer := 0;
max_steps integer := 100;
up_ht numeric;
down_ht numeric;
ttc numeric;
BEGIN
LOOP
EXIT WHEN i > max_steps;
up_ht := round(ht + (i * step), 2);
ttc := round(up_ht * taxes, 2);
IF mod(ttc * 100, 5) = 0 THEN
RETURN up_ht;
END IF;
IF i > 0 THEN
down_ht := round(ht - (i * step), 2);
IF down_ht > 0 THEN
ttc := round(down_ht * taxes, 2);
IF mod(ttc * 100, 5) = 0 THEN
RETURN down_ht;
END IF;
END IF;
END IF;
i := i + 1;
END LOOP;
RETURN ht; -- fallback if nothing is found
END;
$$ LANGUAGE plpgsql IMMUTABLE;
Example with 21% VAT
The get_nearest_ht_multiple_05 function is applied across a price range from €0.00 to €100.00, in steps of €0.01. For each HT price, we check if within the next 100 cents, there is a value that results in a TTC rounded to a multiple of €0.05.
VAT used: 1.21 (i.e., 21%) Criteria: round(HT × 1.21, 2) mod 0.05 = 0
Result
- Total tested: 10,001
- Unchanged (no adjustment needed): 2,001
- Adjusted HT prices: 8,000
- Maximum HT deviation: -€0.06 or +€0.06
Deviation Analysis
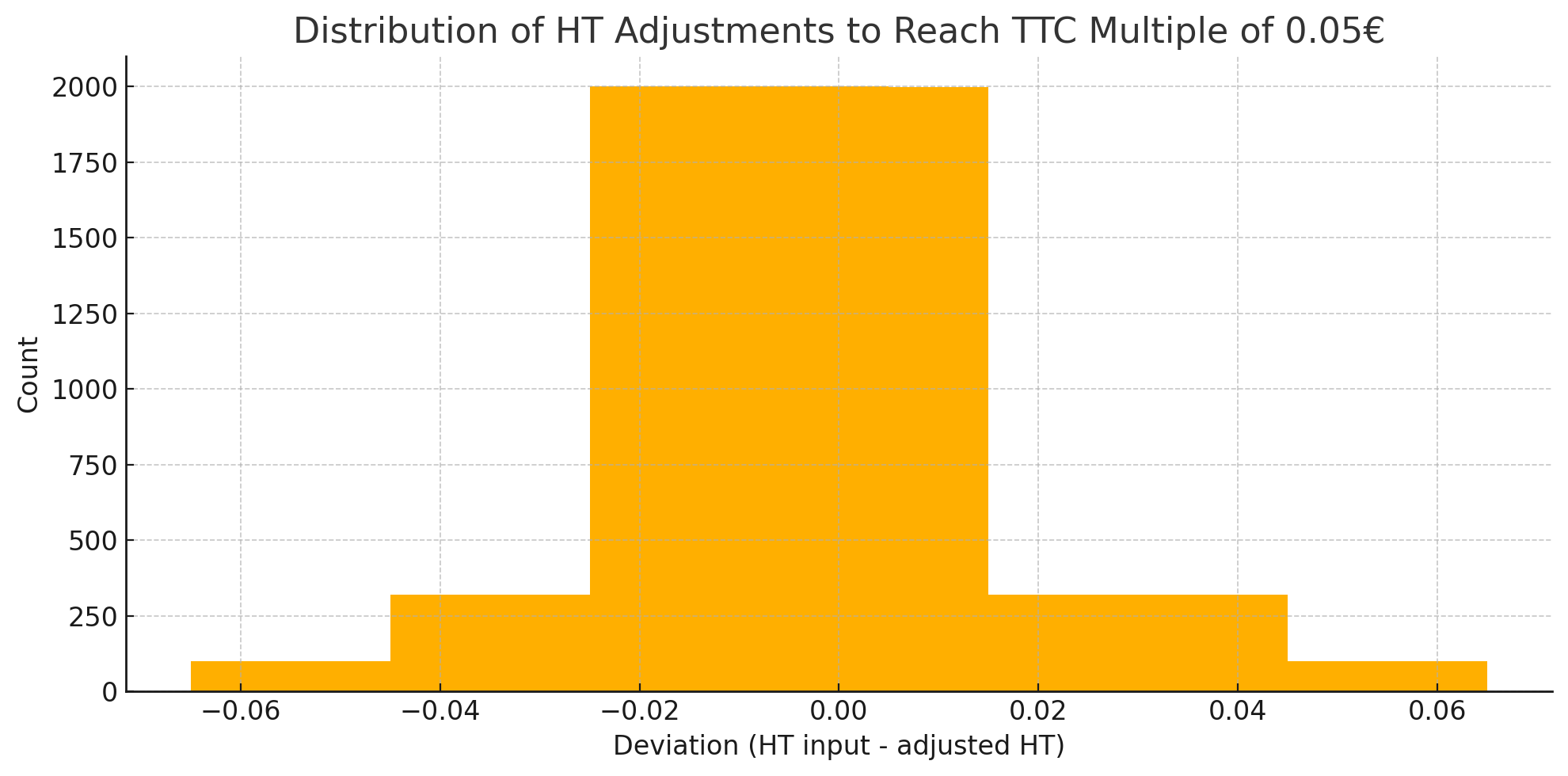
| Deviation | Count |
|---|---|
| -0.06 | 100 |
| -0.05 | 100 |
| -0.04 | 320 |
| -0.03 | 321 |
| -0.02 | 2,000 |
| -0.01 | 2,000 |
| 0.00 | 2,001 |
| 0.01 | 1,999 |
| 0.02 | 320 |
| 0.03 | 320 |
| 0.04 | 320 |
| 0.05 | 100 |
| 0.06 | 100 |